决策树完整代码想抄作业的同学直接点这里
一、决策树简介
决策树是一个很简单的机器学习算法,可以看作if-then的集合,比如我们判断一个西瓜的好坏?我们很可能通过一系列的问题进行判断,比如首先我们问西瓜是绿色的吗?如果是接下来问西瓜甜不甜呢?这就是一颗决策树.
决策树算法,主要由两部分组成:
- 划分选择
- 决策树的生成
下面,将从这两方面进行介绍,并提供对应的python代码,以及手写一颗决策树.
二、划分选择
我们首先要想西瓜的哪个特征对结果影响最大呢?也就是说,先问最关键的问题. 这时候需要引入一个概念信息增益
在介绍信息增益前,先要了解信息熵是什么?
信息熵(entropy): 是度量样本集合纯度的一种最常用的指标,简单说就是这是事件的不确定性的大小,熵越大事件就越不确定,熵为0时,说明这是一个确定性事件。
计算方法: $$ D = [P_1,P_2,...,P_n] $$ $$ Ent(D) = -\sum_{i=1}^n P_i log_2P_i $$
计算示例1: 有一个不均匀硬币,其中正面向上的概率为$\frac{1}{3}$,反面向上的概率也是$\frac{2}{3}$,则该事件的熵的计算公式如下:
$$ Ent(D) = - ( \frac{1}{3} log_2\frac{1}{3} + \frac{2}{3} log_2\frac{2}{3} ) = 0.918$$
计算示例2: 有一个均匀硬币,其中正面向上的概率为$\frac{1}{2}$,反面向上的概率也是$\frac{1}{2}$,则该事件的熵的计算公式如下:
$$ Ent(D) = - ( \frac{1}{2} log_2\frac{1}{2} + \frac{1}{2} log_2\frac{1}{2} ) = 1 $$
可以看到均匀硬币,有更大的信息熵,所以均匀硬币不确定的结果也就越大。
接下来就可以说一下信息增益了,信息增益就是得知信息A而使事件D不确定性,减小的程度,用公式表示为$ g(D,X) = Ent(D) - Ent(D|A) $.
举个例子:假如刚开始有一枚硬币,我们认为硬币是均匀的,所以信息熵为1,但是经过测量我们发现硬币是不均匀的,不均匀程度如上面的计算示例1所示,所以现在的信息熵为0.918.最终我们知道了这个信息的信息增益为$1-0.918=0.082$
计算信息熵的代码如下所示:
|
|
三、决策树的生成
决策树的种类有多种多样,先放一个通用的决策树的为代码,其中红色标注的我们已经学会了

我们可以将书中的伪代码,进一步抽象可以分为下面几个步骤
- 如果数据集中样本为同一类别或者没有特征可以继续划分,停止划分为叶结点赋值
- 选择最优划分属性
- 以最优属性将原数据集分为两个数据集,递归构建决策树
接下来我们说一下决策树中经典算法ID3算法,其实不同的决策树主要的区别就在于第2步,ID3算法使用信息增益来作为评价最优属性的标准。
举个例子
数据集如下所示,使用ID3算法构建决策树.
| 编号 | 敲声 | 颜色 | 好瓜 |
|---|---|---|---|
| 1 | 响 | 绿色 | 是 |
| 2 | 不响 | 绿色 | 是 |
| 3 | 响 | 黄色 | 不是 |
步骤1: 查看数据集是否都是同一类别,答案不是
步骤2: 寻找最优划分属性 初始信息熵为: $$ Ent = -(\frac{2}{3} log_2 \frac{2}{3} + \frac{1}{3} log_2 \frac{1}{3}) = 0.918 $$
假设以敲声划分,敲声响中(1好瓜,1坏瓜),敲声不响中(1好瓜,0坏瓜),计算公式如下所示:
$$ Ent(敲声) = - \frac{2}{3} (\frac{1}{2} log_2 \frac{1}{2} + \frac{1}{2} log_2 \frac{1}{2}) - \frac{1}{3} (\frac{1}{1} log_2 \frac{1}{1} + \frac{0}{1} log_2 \frac{0}{1}) = 0.666 + 0 = 0.666 $$
Warning
在计算的过程中,规定$\frac{0}{1} log_2 \frac{0}{1} = 0$
假设以颜色划分,绿色中(2好瓜,0坏瓜),黄色中(0好瓜,1坏瓜),计算公式如下所示:
$$ Ent(颜色) = - \frac{2}{3} (\frac{2}{2} log_2 \frac{2}{2} + \frac{0}{2} log_2 \frac{0}{2}) - \frac{1}{3} (\frac{0}{1} log_2 \frac{0}{1} + \frac{1}{1} log_2 \frac{1}{1}) = 0 + 0 = 0$$
敲声的信息增益为: $ 0.918 - 0.666 = 0.252 $
颜色的信息增益为: $ 0.918 - 0 = 0.918 $
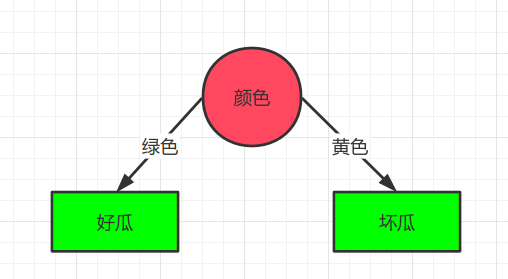
所以颜色为决策树的根节点,接下来我们考虑该节点的儿子节点.
步骤3: 划分数据集
使用颜色划分数据集,划分规则是相同颜色的数据为一个数据集。
即下标为1,2的是数据集S1,下标为3的是数据集S2
步骤4: 查看数据集S1,S2是否都是同一类别,答案是,所以停止划分,我们发现数据集S1全部为好瓜所以该节点为绿色,而另一个节点为坏瓜,最终决策树如下图所示: